Intervall (musik)
Intervall (från lat. intervallum - gap, avstånd; skillnad, olikhet) i musik - förhållandet mellan två musikaliska ljud efter deras höjd [1] . I europeisk musikteori har hela tonen varit ett mått på att beräkna musikaliska intervall i århundraden , i förhållande till vilka både mindre (till exempel halvton , kvartton) och några större (till exempel diton , halvton , triton ) intervaller bestämdes. Det minsta musikaliska intervallet i den europeiska traditionen anses vara en halvton . Intervaller mindre än en halvton kallas mikrointervall.. Konsonant- och dissonantintervall är de viktigaste delarna av harmoni .
Två sidor av intervallet
Å ena sidan kan intervallet representeras som ett matematiskt ( akustiskt ) värde, som uttrycker förhållandet mellan två tal - frekvenserna för huvudövertonerna för de ljud som ingår i det . I de teoretiskt "korrekta", det vill säga de mest naturligt klingande intervallen, bör frekvenserna relateras till små heltal, till exempel 3:2 för en femtedel [2] [3] . Vid lika temperament avviker förhållandena något från "korrekt" (säg 1,498307 istället för 3:2). Ibland, istället för förhållandet, används ekvivalentvärdet för skillnaden i logaritmerna för frekvenserna ( cent för 3:2). Det absoluta matematiska värdet av intervallet fastställs genom mekaniska (på ett monochord , etc.) eller elektroniska (med hjälp av ett applicerat datorprogram) mätningar.
Å andra sidan är intervallet en kategori av specifikt musikalisk logik, som redan visar sig i musikalisk terminologi. Till exempel antyder termen quinta konceptet med fem steg på den diatoniska skalan (det femte steget [quinta vox] beräknas från basen av intervallet, som kallas "prima"). Ur det sammanhang som notskrift ger (bokstav, linjär etc.) är det det musikaliskt-logiska värdet av intervallet som härleds.
Ett intervall som en matematisk (akustisk) storhet kan inte entydigt associeras med ett noterat musikintervall. Till exempel tolkas notationen eis-a ("mi skarp" - "la") i den klassiska harmoniläran som ett kromatiskt intervall (reducerad kvart , vilket betyder upplösningen av mi skarp i f skarp), enharmonisk lika med dur tredjedel av ett enhetligt temperament , i ett annat sammanhang kan det betyda både den pythagoriska ditonen och den stora tredjedelen av den rena skalan (till exempel i den italienska madrigalen på 1500-talet). Intervallet, noterat som fis-a ("F skarpt" - "la"), i tonarten C-dur (C-dur) kan betraktas som en liten tredjedel av ett jämnt härdat system, och i tetrachordet i den kromatiska släktet bland grekerna - som en halvtoraton, eller halvditon , etc.
Eftersom notationen endast fixerar den musikaliska (och inte den matematiska) sidan av intervallen, är frågan om den akustiska "äktheten" av ljudet av den eller den musiken ( särskilt tidig musik ) inte vettig. Tvetydigheten i förhållandet mellan "talet" och den " harmoniska logiken" i intervallet öppnar utrymme för musikologiska och utförande tolkningar av noterad musik.
Klassificering av intervaller
Det nedre ljudet av intervallet kallas bas, det övre ljudet kallas toppen. Intervaller är klassificerade:
1. Genom att ta: simultan (harmonisk, eller "vertikal", intervall) eller sekventiell (melodisk, eller "horisontell", intervall) [4] .
2. Med hjälp av volymen (antal) steg som ingår i dem . Siffran som anger antalet steg i ett intervall är också en förkortning för det intervallet. Intervaller från prima till oktav kallas enkla , ovanför en oktavsammansättning . Sammansatta intervall ärver egenskaperna hos enkla (till exempel kan inga, som sekunder, vara stora och små) [5] . Intervaller som är bredare än en dubbeloktav (kvintdecim) räknas traditionellt inte med i elementär musikteori.
3. Med "kvalitet". Ett intervalls "kvalitet" bestäms av orden "stor" (förkortad b. ), "liten" ( m. ), "ren" ( h. ), "ökad" ( uv. ), "minskad" ( min. . ), "två gånger ökad" ( dv. uv. ) och "två gånger reducerad" ( dv. um. ), vilket förtydligar intervallets kvantitativa karaktäristika.
- Termerna "stor" och "liten" hänvisar till intervallen sekunder, tredjedelar, sjättedelar och sjundedelar.
- Termen "ren" syftar på intervallen prima, kvarts, kvint och oktaver.
4. Enligt graden av eufoni. Från antiken till dur-molltonalitetens tidevarv fördelades även intervaller efter hur sömlöst de uppfattas av örat (för mer information, se artikeln Konsonans och dissonans ). I olika historiska klassificeringar pekade teoretiker ut (i ordning från de mest välljudande till de mest dissonanta) "perfekta konsonanser", "imperfekta konsonanser", "imperfekta dissonanser", "perfekta dissonanser" och andra evaluerande termer.
Ökade och minskade intervaller
I elementär dur-moll musikteori innebär termerna "minskade" och "ökade" intervall en förändring i antalet toner i ett intervall, medan antalet steg förblir oförändrat [6] .
- Ökad - huvudtypen av intervall (ren eller stor) ökas med en halvton.
- Reducerad - huvudtypen av intervall (ren eller liten) sänks med en halvton (förutom "prima").
- Dubbel förstärkt - huvudtypen av intervall (ren eller stor) ökas med en hel ton.
- Två gånger minskad - huvudtypen av intervall (ren eller liten) reduceras med en hel ton (förutom "prima" och "moll sekund").
Exempel:
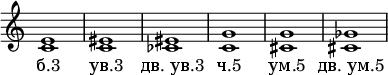
I musik där det inte finns någon dur-moll tonalitet (till exempel i dodekafonin för kompositörer från New Vienna School) förlorar termerna "reducerad" och "ökad" sin betydelse, och termen "ren" används endast i känsla av akustisk renhet (se Pure tuning ).
Lista över musikaliska intervall
Följande tabeller illustrerar typerna av intervall som de standardmässigt beskrivs i handböcker om elementär musikteori från 1900-talet (till exempel i ETM av B. Alekseev och A. Myasoedov [7] ).
| Antal steg |
namn | Typer | Antal toner |
Beteckning |
|---|---|---|---|---|
| Enkla intervaller | ||||
Exempel på enkla harmoniska intervall:
| ||||
| ett | Prima | rena | 0 ( unisont ) | del 1 |
| 2 | Andra | liten stor |
0,5 ( halvton ) 1 ( helton ) |
m.2 b.2 |
| 3 | Tredje | liten stor |
1,5 ( halv-diton ) 2 ( diton ) |
m.3 b.3 |
| fyra | Quart | nätet förstorat |
2,5 3 ( triton ) |
del 4 uv.4 |
| 5 | Kvint | minskat netto |
3 (triton) 3,5 |
sinne.5 h.5 |
| 6 | Sjätte | liten stor |
4 4.5 |
m.6 b.6 |
| 7 | Sjunde | liten stor |
5 5,5 |
m.7 b.7 |
| åtta | Oktav | rena | 6 | del 8 |
| Sammansatta intervall | ||||
Exempel på sammansatta övertonsintervall:
| ||||
| 9 | Nona (andra + h.8) | liten stor |
6,5 7 |
m.9 b.9 |
| tio | Decima (tredje + del 8) | liten stor |
7,5 8 |
m.10 f.10 |
| elva | Undecima (quart + del 8) | nätet förstorat |
8,5 9 |
del 11 uv.11 |
| 12 | Duodecima (femte + del 8) | minskat netto |
9 9,5 |
sinne.12 h.12 |
| 13 | Tertsdecima (sexta + del 8) | liten stor |
10 10,5 |
m.13 f.13 |
| fjorton | Quartdecima (septima + del 8) | liten stor |
11 11,5 |
m.14 f.14 |
| femton | Quintdecima (oktav + h.8) | rena | 12 | del 15 |
| Antal steg | namn | Kvalitet | Antal toner | Beteckning | Quint steg |
| ett | Prima | rena | 0 | del 1 | 0 |
| förstorad | 0,5 | SW.1 | 7 | ||
| 2 | Andra | små | 0,5 | m.2 | 5 |
| stor | ett | b.2 | 2 | ||
| förstorad | 1.5 | SW.2 | 9 | ||
| nedsatt | 0 | sinne.2 | 12 | ||
| 3 | Tredje | små | 1.5 | m.3 | 3 |
| stor | 2 | b.3 | fyra | ||
| nedsatt | ett | sinne.3 | tio | ||
| förstorad | 2.5 | SW.3 | elva | ||
| fyra | Quart | rena | 2.5 | del 4 | ett |
| förstorad | 3 | SW.4 | 6 | ||
| nedsatt | 2 | sinne.4 | åtta | ||
| 5 | Kvint | rena | 3.5 | del 5 | ett |
| nedsatt | 3 | sinne.5 | 6 | ||
| förstorad | fyra | SW.5 | åtta | ||
| 6 | Sjätte | små | fyra | m.6 | fyra |
| stor | 4.5 | b.6 | 3 | ||
| nedsatt | 3.5 | sinne.6 | elva | ||
| förstorad | 5 | SW.6 | tio | ||
| 7 | Sjunde | små | 5 | m.7 | 2 |
| stor | 5.5 | b.7 | 5 | ||
| förstorad | 6 | SW.7 | 12 | ||
| nedsatt | 4.5 | sinne.7 | 9 | ||
| åtta | Oktav | rena | 6 | del 8 | 0 |
| nedsatt | 5.5 | sinne.8 | 7 |
I tolvstegssystemet med lika temperament , som har blivit det främsta inom europeisk musik sedan 1700-talet, beräknas förhållandet mellan frekvenserna för ljuden som bildar intervallet som , där är antalet toner (se tabellen ovan) .
Överklaganden
Inversionen av ett intervall är rörelsen av ljudet som ligger vid dess bas, en oktav upp eller toppen av intervallet - en oktav ner. När det inverteras, är kvaliteten på intervallet omvänd: ett stort blir litet, ett förstorat intervall minskas, ett dubbelt ökat intervall blir två gånger minskat och vice versa. Ett rengöringsintervall förblir rent. I enkla intervall är summan av de digitala beteckningarna för huvudtypen av intervall och dess invertering alltid lika med nio.
| Grundläggande avstånd | Inverterat intervall |
|---|---|
| Prima (1) | Oktav (8) |
| Andra (2) | Septima (7) |
| Tredje (3) | Sexta (6) |
| Quart (4) | Quinta (5) |
| Quinta (5) | Quart (4) |
| Sexta (6) | Tredje (3) |
| Septima (7) | Andra (2) |
| Oktav (8) | Prima (1) |
Om det krävs att vända ett sammansatt intervall överförs båda dess ljud till en oktav (övre - ner, nedre - upp) eller en av dem till två oktaver, medan summan av de digitala beteckningarna för båda intervallen alltid är lika med sexton.
| Grundläggande avstånd | Inverterat intervall |
|---|---|
| Nona (9) | Septima (7) |
| Decima (10) | Sexta (6) |
| Undecima (11) | Quinta (5) |
| Duodecyma (12) | Quart (4) |
| Terzdecima (13) | Tredje (3) |
| Quartdecima (14) | Andra (2) |
| Quintdecima (15) | Prima (1) |
En ökad oktav, även betraktad som ett sammansatt intervall, ger en minskad oktav i cirkulationen.
Anteckningar
- ↑ Nazaikinsky E. V. Interval Arkivkopia daterad 16 april 2018 på Wayback Machine // Great Russian Encyclopedia. Volym 11. - M., 2008. - S. 435.
- ↑ I inhemsk musikvetenskap kallas det numeriska förhållandet mellan intervallet ofta felaktigt för " proportion ". Till exempel E.V. Gertsman: "... ljud bör uttryckas med ett tal... man kan säkert representera sunda relationer med specifika numeriska proportioner. Men eftersom ojämna kvantitetsförhållanden representeras av olika typer av proportioner, kan avstånden mellan ljud (intervall) registreras på ett liknande sätt, det vill säga multipla, epimorala, epimera och andra proportioner ”(Pythagorean musicology. SPb., 2003, s. 280-281.).
- ↑ Detaljer om de aritmetiska termerna "ratio" och "proportion" kan hittas i aritmetiska läroböcker, till exempel i det sjätte avsnittet av A. S. Kiselevs lärobok "Systematic Arithmetic Course" Arkivexemplar daterad 4 december 2016 på Wayback Machine .
- ↑ Termerna "horisontellt intervall" och "vertikalt intervall" kom i bruk under de sista decennierna av 1900-talet, se till exempel: Kholopov Yu. N. Harmony. Teoretisk kurs. M., 1988, s. 22. I de hittills populära läroböckerna i elementär musikteori, skrivna på 1950-talet. - I. V. Sposobina (1951), V. A. Vakhromeev (1956), såväl som i "Praktisk guide till musikalisk läskunnighet" av G. A. Fridkin (1957) - endast termerna (respektive) "melodisk intervall" och "harmoniskt intervall.
- ↑ Intervall // Kazakstan. Nationalencyklopedin . - Almaty: Kazakiska uppslagsverk , 2005. - T. II. — ISBN 9965-9746-3-2 . (CC BY SA 3.0)
- ↑ Alekseev, Myasoedov, 1986 , sid. 69.
- ↑ Alekseev, Myasoedov, 1986 , sid. 67, 70.
- ↑ Bityukov Sergey. 13 ljud och intervaller. Deras uppfattning och beteckning. Frets av avvikelse och modulering (ryska) ? . Habr (7 augusti 2021). Hämtad 12 augusti 2021. Arkiverad från originalet 12 augusti 2021.
Litteratur
- Alekseev B., Myasoedov A. Intervaller // Elementär musikteori. - M . : Musik, 1986. - S. 64-78. — 240 s.
- Intervall // Musical Encyclopedia. - M . : Soviet Encyclopedia, 1974. - T. 2. - S. 544-545. — 960 sid.
- Solovyov N.F. Interval // Encyclopedic Dictionary of Brockhaus and Efron : i 86 volymer (82 volymer och ytterligare 4). - St Petersburg. 1890-1907.
- Fridkin G. En praktisk guide till musikalisk läskunnighet. — M.: Muzgiz, 1962
Länkar
- Hugo Riemanns intervalltabeller
- Tabell 365 över intervall (namn på intervall och deras översättningar är inte normativa)
| |
|
|---|---|
| I bibliografiska kataloger |
|
| Musikaliska intervaller | ||
|---|---|---|
| Enkel | ||
| Sammansatt | ||
| Mikrointervaller | ||
| Särskild | ||




